mathic.com: Krzysztof Wesołowski - Kurs: [30h] Matematyka - Zajęcia: Wykład 4 - Ciągi liczbowe [dokończenie poprzedniego wykładu] (granica właściwa, niewłaściwa, ciąg geometryczny, własności, symbole oznaczone i nieoznaczone, twierdzenie o dwóch ciągach, o trzech ciągach, granice specjalne)

Kurs: [30h] Matematyka - Wykład

Temat: Wykład 4 - Ciągi liczbowe [dokończenie poprzedniego wykładu] (granica właściwa, niewłaściwa, ciąg geometryczny, własności, symbole oznaczone i nieoznaczone, twierdzenie o dwóch ciągach, o trzech ciągach, granice specjalne)

Data zajęć: 2019-10-25

Ogłoszenia: 9:15-10:45

Treść zajęć

Granice ciągów liczbowych

Komentarz
Zastanowimy się, jak zachowuje się ogon ciągu $(a_n)$ (innymi słowy wyrazy ciągu $a_n$ , gdy $n$ rośnie nieograniczenie - mówimy, że $n$ ucieka do nieskończoności).

Granica właściwa ciągu liczbowego

Na rysunku widzimy ciąg o wyrazach dodatnich, którego wyrazy, wraz ze wzrostem wartości $n$ , coraz bardziej zbliżają się do liczby zero (w tym przypadku nigdy tej wartości nie osiągając). Można to określić, że ogon ciągu "zbiega" do wartości zero. Ponadto mimo, że zero jest nie osiągnięte, bez względu na to jak małą (bliską zeru) wybierzemy liczbę $\varepsilon > 0$ , to nieskończenie wiele wyrazów ciągu (jego ogon, od pewnego miejsca) leży w przedziale $\lbrack - \varepsilon, \varepsilon\rbrack$ .

Definicja (Granica ciągu liczbowego)
Ciąg liczbowy $(a_n)$ ma granicę właściwą $g\in\mathbb{R}$ , co zapisujemy $\lim_{n\to\infty} a_{n}=g$ lub $a_{n}\xrightarrow[]{n\to\infty} g$ , wtedy i tylko wtedy, gdy $\forall \varepsilon>0 \; \exists n_0\in\mathbb{N} \; \forall n\in\mathbb{N} \; \left(n\geq n_0 \implies |a_n-g|\leq \varepsilon\right)$

Oznaczenie
Ciąg nazywam zbieżnym, jeśli posiada granicę właściwą.

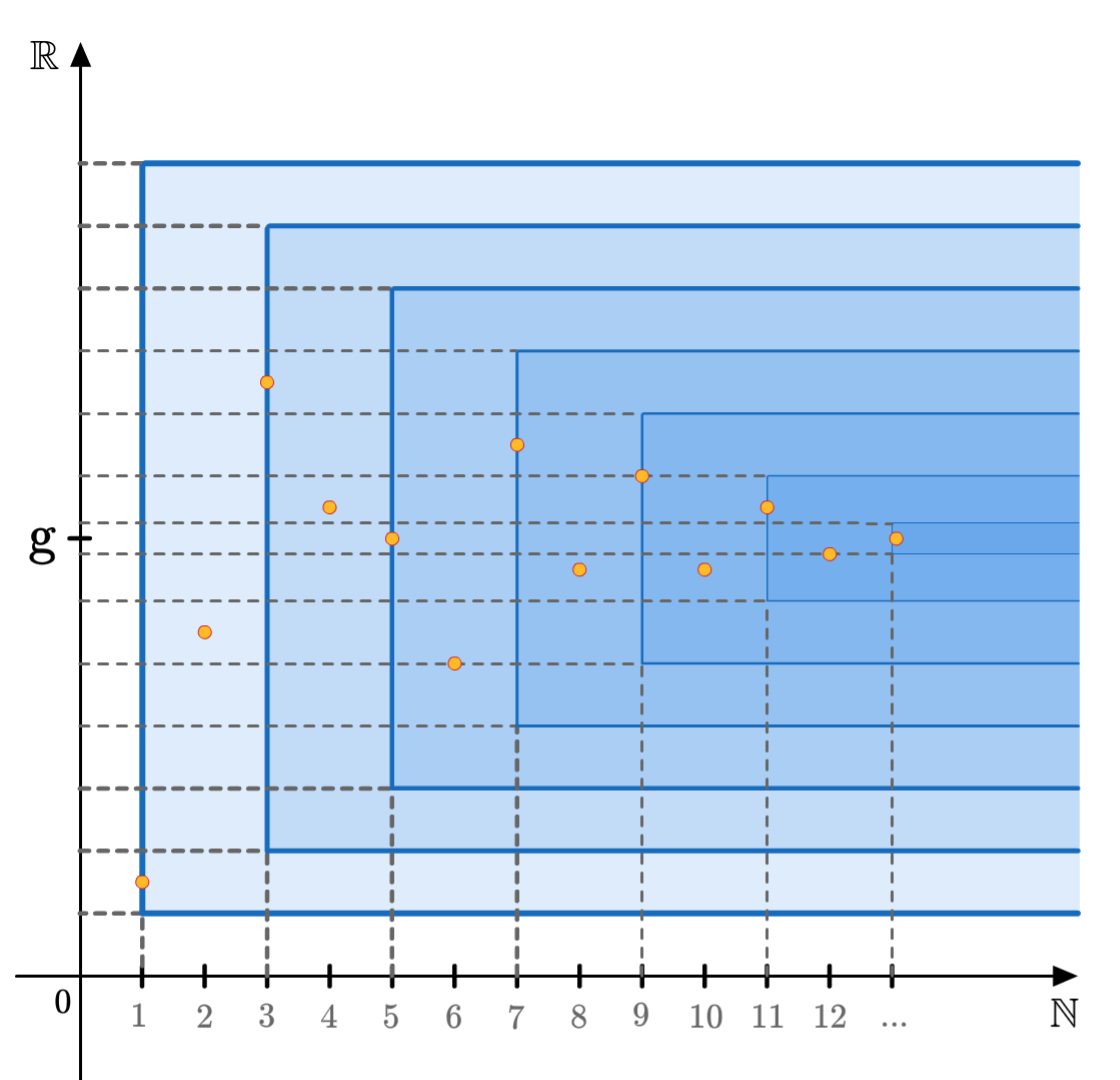Można rozumieć, że ciąg $(a_n)$ zbiega go granicy $g$ , gdy w dowolnie wąskim pasie (o środku w $g$ i szerokości $2\varepsilon$ ) leży ogon ciągu $(a_n)$ .

Przykład
Pokażać, korzystając z definicji granicy, że $\lim_{n\rightarrow\infty} \frac{1}{n}= 0$ .
Rozwiązanie: Aby wykazać, że liczba $0$ jest granicą ciągu $(a_n)=(\frac{1}{n})$ weźmy dowolną liczbę $\varepsilon > 0$ i wykażmy, że uda się znaleźć taką liczbę naturalną $n_0$ , że dla wszystkich $n \geq n_0$ zachodzi nierówność $|a_n-0| < \varepsilon$ . Zauważmy w tym celu, że zachodzą ograniczenia $|\frac{1}{n}-0|=\frac{1}{n} < \varepsilon$ dla $n>\frac{1}{\varepsilon}$ , zatem $\frac{1}{\varepsilon}$ mogłoby być naszym wstępnym kandydatem na $n_0$ , jednakże ponieważ nie ma gwarancji że jest to liczba naturalna, to możemy przyjąć ewentualnie "ciut" więcej, mianowicie $n_0 = \lbrack \frac{1}{\varepsilon}\rbrack + 1$ , gdzie $[x]$ oznacza część całkowitą z liczby rzeczywistej $x$ . Dla tak dobranego $n_0$ i dowolnej liczby $n \geq n_0$ zachodzi wtedy nierówność $\frac{1}{n} < \varepsilon$ , czyli $|a_n-0| < \varepsilon$ , a to właśnie mieliśmy wykazać.

Ćwiczenie
Pokażać, korzystając z definicji granicy, że:

a) $\lim_{n \rightarrow \infty} \frac{1-3 n}{1+n}=-3$

b) $\lim_{n \rightarrow \infty} \frac{1}{2^{n}+1}=0$

c) $\lim_{n \rightarrow \infty} \sqrt[n]{a}=1$ dla $a>0$

d) $\lim_{n \rightarrow \infty} \sin \frac{1}{n}=0$

Twierdzenie (O jednoznaczności granicy ciągu liczbowego)
Ciąg zbieżny ma dokładnie jedną granicę.

Rysunek pokazuje, że ciąg nie może mieć dwóch różnych granic.

Granica niewłaściwa ciągu liczbowego

Definicja (Granica niewłaściwa $+\infty$ )
Ciąg liczbowy $(a_n)$ ma granicę niewłaściwą $+\infty$ , co zapisujemy $\lim_{n\to\infty} a_{n}=+\infty$ lub $a_{n}\xrightarrow[]{n\to\infty} +\infty$ , wtedy i tylko wtedy, gdy $\forall M>0 \; \exists n_0\in\mathbb{N} \; \forall n\in\mathbb{N} \; \left(n\geq n_0 \implies a_n\geq M\right)$

Oznaczenie
Ciąg, mający granicę niewłaściwą $+\infty$ , nazywam zbieżnym do $+\infty$ (niektórzy autorzy określają go jako rozbieżny do $+\infty$ ).

Definicja (Granica niewłaściwa $-\infty$ )
Ciąg liczbowy $(a_n)$ ma granicę niewłaściwą $+\infty$ , co zapisujemy $\lim_{n\to\infty} a_{n}=-\infty$ lub $a_{n}\xrightarrow[]{n\to\infty} -\infty$ , wtedy i tylko wtedy, gdy $\forall m<0 \; \exists n_0\in\mathbb{N} \; \forall n\in\mathbb{N} \; \left(n\geq n_0 \implies a_n\leq m\right)$

Oznaczenie
Ciąg, mający granicę niewłaściwą $-\infty$ , nazywam zbieżnym do $-\infty$ (niektórzy autorzy określają go jako rozbieżny do $-\infty$ ).

Rysunek przedstawia wykresy ciągów liczbowych, mających granice niewłaściwe - po lewej $+\infty$ , po prawej $-\infty$ .

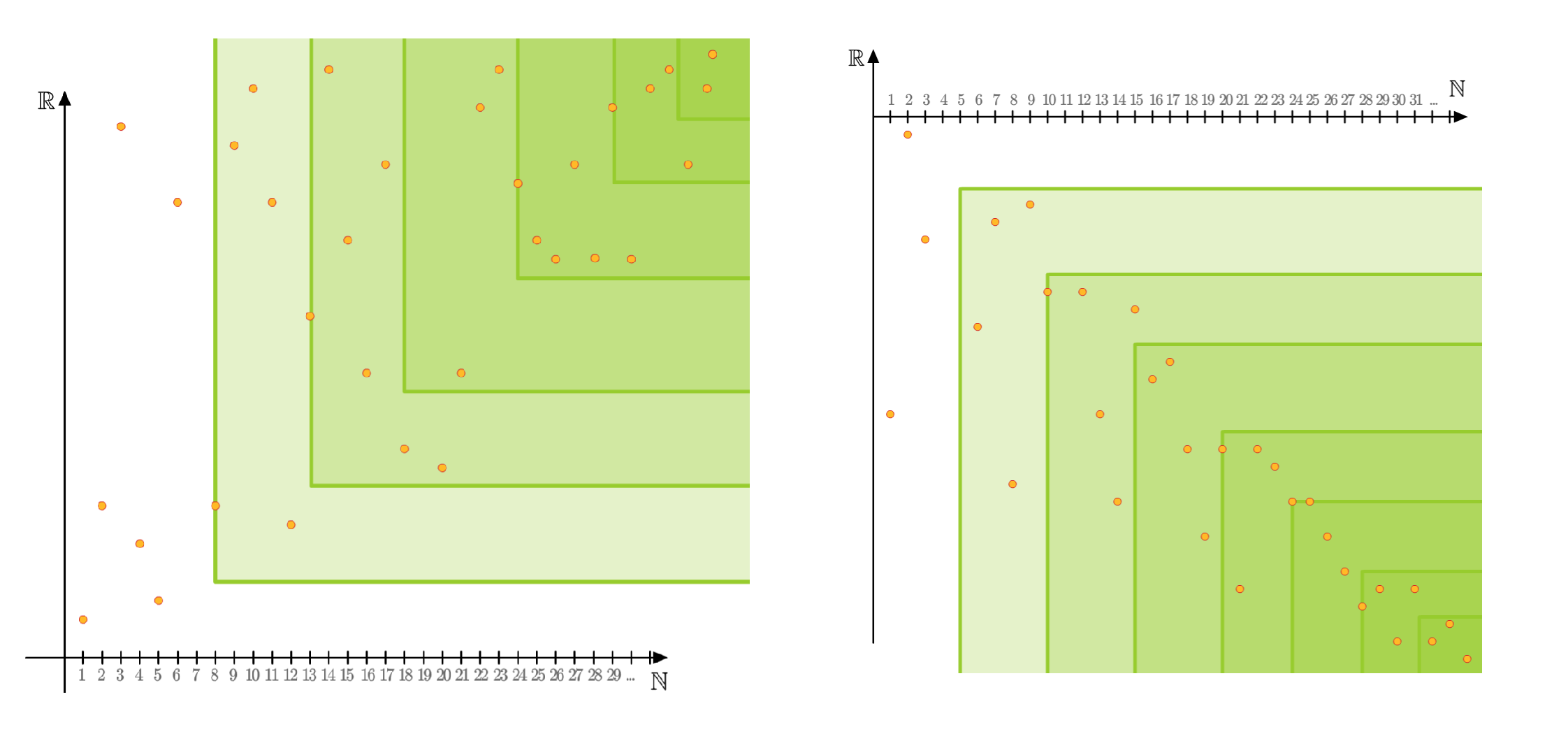Można rozumieć, że ciąg liczbowy ma granicę niewłaściwą $+\infty$ , jeśli na wykresie jego ogon ucieka nieograniczenie w górę. Z kolei ciąg liczbowy ma granicę niewłaściwą $-\infty$ , gdy wszystkie dostatecznie dalekie wyrazu ciągu są mniejsze od dowolnie małej liczby.

Definicja (Ciąg rozbieżny)
Ciąg, który nie posiada granicy właściwej ani niewłaściwej nazywamy ciągiem rozbieżnym.

Rysunek przedstawia ciąg rozbieżny. Nie ma on ani granicy właściwej (skończonej), ani (jako całość) nie ucieka do $+\infty$ ani do $-\infty$ .

Przykład
Wykazać, że ciąg $a_n=(-1)^n$ jest rozbieżny.
Rozwiązanie: Zauważmy, że ciąg $(a_n)$ przyjmuje na zmianę wartości 1 albo -1. Nie może to być ciąg zbieżny do $+ \infty$ , bo dla $M=2$ żaden wyraz ciągu nie jest większy od $M$ i analogicznie nie może być zbieżny do $- \infty$ , bo żaden wyraz ciągu nie jest mniejszy od $-M$ . Żadna liczba rzeczywista $g$ różna od 1 i -1 nie może też być granicą właściwą ciągu $(a_n)$ , bo jeżeli wybierzmy przedział $(g- \varepsilon,g+ \varepsilon)$ , który nie zawiera liczb 1 i -1, to nie zawiera też żadnego wyrazu naszego ciągu. Liczba 1 też nie może być granicą właściwą ciągu $(a_n)$ , ponieważ poza przedziałem $(1- \varepsilon,1+ \varepsilon)$ , który nie zawiera liczby -1 leży nieskończenie wiele wyrazów naszego ciągu. Analogicznie liczba -1 nie może być granicą właściwą ciągu $(a_n)$ . Zatem ciąg $(a_n)$ nie ma zarówno granicy właściwej, jak i niewłaściwej, czyli jest rozbieżny.

Ćwiczenie
Korzystając z definicji granicy niewłaściwej, uzasadnić poniższe równości:

a) $\lim _{n \rightarrow \infty}\left(2^{n}-5\right)=\infty$

b) $\lim _{n \rightarrow \infty} \frac{n^{2}}{2 n-1}=\infty$

b) $\lim _{n \rightarrow \infty}\left(3-\log _{2} n\right)=-\infty$

Spostrzeżenie
Granica właściwa lub niewłaściwa ciągu lub jego rozbieżność nie zależą od zachowania dowolnej skończonej liczby początkowych wyrazów ciągu.

Ćwiczenie
Ocenić, czy poniższe ciągi są zbieżne do granicy właściwej lub niewłaściwej (czy interesuje nas $n\leq 2000$ ?):

a) $a_{n}=\left\{\begin{array}{ll}{(-1)^{n}} & {\text { dla } \quad n \leq 2000} \\ {\frac{n^{2}}{n^{2}+1}} & {\text { dla } \quad n>2000}\end{array}\right.$

b) $b_{n}=\left\{\begin{array}{ll}{\frac{1}{n}} & {\text { dla } \quad n \leq 2000} \\ {3^{n}} & {\text { dla } \quad n>2000}\end{array}\right.$

Ciąg geometryczny

Uwaga (Granica ciągu geometrycznego)
Ciąg geometryczny $(q^n)$ może być zbieżny lub rozbieżny, w zależności od wartości $q$ . Zachodzi bowiem $\lim _{n \rightarrow \infty} q^{n}\left\{\begin{array}{ll}{=0} & {\text { dla } \quad|q|<1} \\ {=1} & {\text { dla } \quad q=1} \\ {=\infty} & {\text { dla } \quad q>1} \\ {\text { nie istnieje }} & {\text { dla } \quad q \leq-1}\end{array}\right.$

Ćwiczenie
Znaleźć granice ciągów:

a) $a_{n}=\left(-\frac{1}{2}\right)^{n}$

b) $b_{n}=3^{n}$

c) $c_{n}=\left(-\frac{5}{4}\right)^{n}$

d) $d_{n}=\left(p^{2}+2 p-2\right)^{n}$ (w zależności od $p$ )

e) $e_{n}=\left(\sin p+\frac{1}{2}\right)^{n}$ (w zależności od $p$ )

Związki pomiędzy zbieżnością a ograniczonością ciągu

Twierdzenie (O ograniczoności ciągu zbieżnego do granicy właściwej)
Każdy ciąg zbieżny do granicy właściwej jest ograniczony.

Ciąg zbieżny do granicy właściwej jest ograniczony, gdyż w dowolnie wąskim pasie znajduje się jego ogon (czyli ogon jest ograniczony), zaś poza ogonem pozostaje skończenie wiele początkowych wyrazów ciągu, z których można wybrać największy i najmniejszy. Stanowią one ograniczenie górne i dolne.

Uwaga
Nie zachodzi twierdzenie odwrotne do powyższego twierdzenia, czyli nie każdy ciąg ograniczony musi być zbieżny do granicy właściwej.

Rysunek uzasadnia, że ograniczoność ciągu nie koniecznie musi implikować jego zbieżność, gdyż przedstawiony jest ciąg ograniczony, nie będący zbieżnym.

Twierdzenie (O nieograniczoności ciągu zbieżnego do granicy niewłaściwej)
Ciąg zbieżny do granicy $+\infty$ nie jest ograniczony od góry, natomiast ciąg zbieżny do granicy $-\infty$ nie jest ograniczony od dołu.

Interpretacja geometryczna braku ograniczoności ciągów zbieżnych do granic niewłaściwych. Z lewej: skoro ciąg ma granicę $+\infty$ , to musi uciekać nieograniczenie "do góry", zatem żadna pozioma "poprzeczka" nie może go ograniczać od góry. Podobnie z prawej: skoro ciąg ma granicę $-\infty$ , to musi uciekać nieograniczenie "w dół", zatem żadna pozioma "poprzeczka" nie może go ograniczać od dołu.

Uwaga
Nie zachodzi twierdzenie odwrotne do powyższego twierdzenia, czyli ciąg, który nie jest ograniczony od góry nie musi być rozbieżny do $+ \infty$ , ani ciąg, który nie jest ograniczony od dołu nie musi być rozbieżny do $- \infty$ .

Własności ciągów

Twierdzenie (O zachowaniu nierówności w granicy)
Jeżeli $\lim_{ n \rightarrow \infty}a_n=a$ i $\lim_{ n \rightarrow \infty} b_n=b$ oraz od pewnego miejsca zachodzą nierówności pomiędzy odpowiednimi wyrazami ciągów $a_n < b_n$ , to pomiędzy granicami ciągów zachodzi nierówność $a \leq b$ .

Rysunek przedstawia na jednym wykresie dwa ciągi zbieżne, z których jeden (czerwony) ma wyrazy od pewnego miejsca większe niż drugi (niebieski). Wydaje się być oczywiste, że granica ciągu o wyrazach większych nie może być mniejsza od granicy ciągu o wyrazach mniejszych. Już nie taki oczywisty jest fakt, że granice te mogą być równe, mimo, że pomiędzy wyrazami zachodzą nierówności silne.

Uwaga
W granicy zachowana jest nierówność o tym zwrocie jak pomiędzy wyrazami dwóch ciągów, ale zawsze jako nierówność słaba.

Twierdzenie (O ciągu ograniczonym i monotonicznym)
Jeżeli ciąg $(a_n)$ jest ograniczony i monotoniczny, to jest zbieżny.

Rysunek przedstawia dwa ciągi ograniczone i monotoniczne, z których jeden jest rosnący (niebieski), a drugi malejący (czerwony). Zauważmy, że obydwa ciągi mają granice właściwe, ciąg rosnący i ograniczony od góry jest zbieżny do najmniejszego swojego ograniczenia górnego, a ciąg malejący i ograniczony od dołu jest zbieżny do największego swojego ograniczenia dolnego.

Przykład
Uzasadnij zbieżność ciągu $a_n= \frac{1}{1 \cdot 2^1}+ \frac{1}{2 \cdot 2^2}+\cdots+\frac{1}{n \cdot 2^n }$ .
Rozwiązanie: Zbadamy monotoniczność ciągu wyznaczając znak różnicy $a_{n+1}-a_n$ . Mamy $a_{n+1}-a_n$ $= \frac{1}{(n+1) \cdot 2^{n+1} }>0$ dla wszystkich $n$ naturalnych. Ponieważ różnica $a_{n+1}-a_n$ jest dodatnia, to ciąg $(a_n)$ jest rosnący. Wystarczy teraz zbadać, czy ciąg jest ograniczony od góry, bo wiemy, że ciąg rosnący jest ograniczony od dołu przez pierwszy wyraz. Wykorzystujemy ograniczenie $a_n$ $= \frac{1}{1 \cdot 2^1 }+\frac{1}{2 \cdot 2^2}+ \cdots + \frac{1}{n \cdot 2^n}$ $<\frac{1}{2^1}+\frac{1}{2^2} + \cdots +\frac{1}{2^n}$ . Zauważamy, że $\frac{1}{2^1} +\frac{1}{2^2} + \cdots +\frac{1}{2^n}$ jest sumą ciągu geometrycznego o pierwszym wyrazie $\frac{1}{2}$ i ilorazie $\frac{1}{2}$ . Ze wzoru na $n$ -tą sumę ciągu geometrycznego mamy $\frac{1}{2^1} +\frac{1}{2^2} + \cdots +\frac{1}{2^n}$ $= \frac{1}{2} \frac{ 1-(\frac{1}{2})^n }{ 1-\frac{1}{2}}$ $=1-(\frac{1}{2})^n<1$ . Z powyższego oszacowania wnioskujemy, że ciąg $(a_n)$ jest ograniczony, zatem twierdzenie mówi, że jest zbieżny.

Przykład
Uzasadnij zbieżność ciągu $b_n= \frac{(n!)^2}{(2n)!}$ .
Rozwiązanie: Badamy monotoniczność ciągu $(b_n)$ zauważając, że jest to ciąg o wyrazach dodatnich, czyli możemy badać iloraz $\frac{b_{n+1}}{b_n}$ $=\frac{[(n+1)!]^2}{(2n+2)!} \frac{(2n)!}{(n!)^2}$ $=\frac{[(n+1) \cdot n!]^2}{(2n+2) \cdot (2n+1) \cdot (2n)!} \frac{(2n)!}{(n!)^2}$ $=\frac{n+1}{2(2n+1)}<1$ . Ponieważ iloraz $\frac{b_{n+1}}{b_n}$ jest dla wszystkich $n$ naturalnych mniejszy od jedynki, to ciąg $(b_n)$ jest malejący. Badamy teraz, czy ciąg $(b_n)$ jest ograniczony od dołu, gdyż wiemy, że ciąg malejący jest ograniczony od góry przez pierwszy wyraz. Zauważamy, że $b_n=\frac{(n!)^2}{(2n)!}>0$ dla wszystkich $n$ naturalnych, zatem ciąg $(b_n)$ jest ograniczony. Na podstawie twierdzenia wnioskujemy, że ciąg $(b_n)$ jest zbieżny.

Symbole oznaczone i nieoznaczone

Definicja (Symbol oznaczony)
Symbolem oznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i które daje zawsze taki sam wynik zależny tylko od granic ciągów, z których powstaje symbol graniczny.

Definicja (Symbol nieoznaczony)
Symbolem nieoznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i którego wartości nie da się jednoznacznie obliczyć, gdyż zależy od rozpatrywanego ciągu.

Twierdzenie (O symbolach oznaczonych $\frac{1}{0}$ i $\frac{1}{\infty}$ )
Zachodzą następujące implikacje:

1. Jeżeli $\lim_{n \rightarrow \infty}|a_n |=0$ , to $\lim_{n \rightarrow \infty} \frac{1}{|a_n |}= + \infty$

2. Jeżeli $\lim_{n \rightarrow \infty}a_n=\pm\infty$ , to $\lim_{n \rightarrow \infty} \frac{1}{a_n} =0$ .

Przykład
Obliczmy granicę $\lim_{n \rightarrow \infty} \frac{1}{n^2+1}$
Rozwiązanie: Mamy $\lim_{n \rightarrow \infty} \frac{1}{n^2+1}$ $= \left[\frac{1}{+\infty}\right]$ $= 0$ .

Twierdzenie (O symbolach oznaczonych)
Niech $a$ będzie dowolna liczbą rzeczywistą. Symbolami oznaczonymi są:

$\lbrack \pm \infty + a \rbrack =\pm \infty$ ,

$\lbrack a \cdot (\pm \infty) \rbrack = \begin{cases} \pm \infty & \text{ dla } a>0 \\ \mp \infty & \text{ dla } a<0 \end{cases}$ ,

$\lbrack \pm \infty \cdot (\pm \infty) \rbrack=+ \infty$ ,

$\lbrack \pm \infty \cdot (\mp \infty) \rbrack =- \infty$ ,

$\Big[\frac{a}{\pm\infty}\Big]=0$ ,

$\Big[\frac{a}{0^\pm}\Big]= \begin{cases} \pm \infty & \text{ dla } a>0 \\ \mp \infty & \text{ dla } a<0 \end{cases}$ ,

$[\infty^a ]= \begin{cases} \infty & \text{ dla } a>0 \\ 0 & \text{ dla } a<0 \end{cases}$ ,

$[\infty^{\infty} ]= \infty$ ,

gdzie symbol $[0^+]$ oznacza granicę ciągu o wyrazach dodatnich zbieżnego do zera, a symbol $[0^-]$ granicę ciągu o wyrazach ujemnych zbieżnego do zera.

Przykład
Obliczmy granicę $\lim_{n \rightarrow \infty} (3n^3-2n^2+n-4)$ .
Rozwiązanie: Mamy $\lim_{n \rightarrow \infty} (3n^3-2n^2+n-4)$ $= \lim_{n \rightarrow \infty} n^3 (3- \frac{2}{n}+ \frac{1}{n^2} - \frac{4}{n^3} )$ $=[\infty \cdot (3-0+0-0)]$ $= \infty$ .

Przykład
Obliczmy granicę $\lim_{n \rightarrow \infty} ( \frac{n^2+1}{n+1})^n$ .
Rozwiązanie: Mamy $\lim_{n \rightarrow \infty} \frac{n^2+1}{n+1}$ $= \lim_{n \rightarrow \infty} \frac{n (1+\frac{1}{n^2}) }{1+\frac{1}{n}}$ $=[ \frac{ \infty \cdot (1+0)}{1+0}]$ $= \infty$ . Obliczamy $\lim_{n \rightarrow \infty} (\frac{n^2+1}{n+1})^n$ $=[\infty^{\infty} ]$ $=\infty$ .

Twierdzenie (O symbolach nieoznaczonych)
Jest siedem symboli nieoznaczonych. Są nimi:

$[ \infty- \infty]$ , $[\frac{0}{0}]$ , $[ \frac{\infty}{\infty}]$ , $[ 0 \cdot \infty]$ , $[ \infty^0]$ , $[0^0]$ , $[1^{\infty}]$ .

Przykład
Pokażmy, że symbol $[0 \cdot \infty]$ jest nieoznaczony.
Rozwiązanie: Mamy:
$\lim_{n \rightarrow \infty} \frac{1}{n^2} \cdot n$ $=[0 \cdot \infty]$ $= \lim_{n \rightarrow \infty} \frac{1}{n}$ $=[\frac{1}{+\infty}]$ $=0$ .
$\lim_{n \rightarrow \infty} \frac{1}{n} \cdot n^2$ $=[0 \cdot \infty]$ $= \lim_{n \rightarrow \infty} n$ $=[+\infty]$ $=+\infty$ .
Świadczy to o tym, że nie da się w sposób jednoznaczny określić wartości symbolu $[0 \cdot \infty]$ .

Przykład
Pokażmy, że symbol $[ \infty - \infty ]$ jest nieoznaczony.
Rozwiązanie: Mamy:
$\lim_{n \rightarrow \infty} (n^3-n)$ $=[ \infty - \infty ]$ $=\lim_{n \rightarrow \infty} n^3 (1- \frac{1}{n^2} )$ $=[ \infty \cdot (1-0) ]$ $= \infty$ .
$\lim_{n \rightarrow \infty} (n-n^3)$ $=[ \infty - \infty ]$ $=\lim_{n \rightarrow \infty}n^3 ( \frac{1}{n^2} -1)$ $=[ \infty \cdot (0-1) ]$ $=- \infty$ .
Różne wyniki dowodzą, że nie da się w sposób jednoznaczny określić wartości symbolu $[ \infty - \infty ]$ .

Działania arytmetyczne na ciągach

Twierdzenie (O działaniach arytmetycznych na ciągach zbieżnych)
Zachodzą równości:

$\lim_{n\to \infty}{(a_n+b_n)}=\lim_{n\to \infty}{a_n}+\lim_{n\to \infty}{b_n}$ (granica sumy ciągów jest równa sumie granic)

$\lim_{n\to \infty}{(a_n-b_n)}=\lim_{n\to \infty}{a_n}-\lim_{n\to \infty}{b_n}$ (granica różnicy ciągów jest równa różnicy granic)

$\lim_{n\to \infty}{(c\cdot a_n)}=c\cdot \lim_{n\to \infty}{a_n}\textrm{ dla dowolnego }c\in \mathbb{R}$ (stałe można wyłączać przed znak granicy)

$\lim_{n\to \infty}{(a_n\cdot b_n)}=\lim_{n\to \infty}{a_n}\cdot \lim_{n\to \infty}{b_n}$ (granica iloczynu to iloczyn granic)

$\lim_{n\to \infty}{\frac{a_n}{b_n}}=\frac{\lim_{n\to \infty}{a_n}}{\lim_{n\to \infty}{b_n}}$ o ile $\lim_{n\to \infty}{b_n} \neq 0$ (granica ilorazu to iloraz granic)

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\left(\frac{3}{n^2}+\frac{2}{n}-5\right)}$ .
Rozwiązanie: Mamy $\lim_{n\to \infty}{\left(\frac{3}{n^2}+\frac{2}{n}-5\right)}$ $=\lim_{n\to \infty}{\left(\frac{3}{n^2}\right)}+\lim_{n\to \infty}{\left(\frac{2}{n}\right)}-\lim_{n\to \infty}{\left(5\right)}$ $=3\lim_{n\to \infty}{\left(\frac{1}{n^2}\right)}+2\lim_{n\to \infty}{\left(\frac{1}{n}\right)}-\lim_{n\to \infty}{\left(5\right)}$ $=[3\cdot 0+2\cdot 0-5]=[0-5]=-5$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\frac{(3n+1)(-2n+4)}{1-3n-2n^2}}$ .
Rozwiązanie:

Mamy $\lim_{n\to \infty}{\frac{(3n+1)(-2n+4)}{1-3n-2n^2}}$ $=\lim_{n\to \infty}{\frac{n^2\left(3+\frac{1}{n}\right)\left(-2+\frac{4}{n}\right)}{n^2\left(\frac{1}{n^2}-\frac{3}{n}-2\right)}}$ $=\left[\frac{(3+0)(-2+0)}{0-0-2}\right]$ $=3$ .

Twierdzenie o dwóch ciągach

Twierdzenie (O dwóch ciągach)
Zachodzą poniższe implikacje:

1. Jeżeli $\lim_{n\to \infty}{a_n}=+\infty$ oraz od pewnego miejsca pomiędzy wyrazami dwóch ciągów zachodzą nierówności $a_n\leq b_n$ , to $\lim_{n\to \infty}{b_n}=+\infty$ .

2. Jeżeli $\lim_{n\to \infty}{b_n}=-\infty$ oraz od pewnego miejsca pomiędzy wyrazami dwóch ciągów zachodzą nierówności $a_n\leq b_n$ , to $\lim_{n\to \infty}{a_n}=-\infty$ .

Rysunek obrazuje podpunkt 1 powyższego twierdzenia. Ciąg czerwony zbieżny do $+\infty$ "wypycha" ciąg niebieski (który jest od czerwonego większy) również do $+\infty$ .

Rysunek obrazuje podpunkt 2 powyższego twierdzenia. Ciąg czerwony zbieżny do $-\infty$ "wypycha" ciąg niebieski (który jest od czerwonego mniejszy) również do $-\infty$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{(3\sin{n}-5)\cdot n^3}$ .
Rozwiązanie: Kłopot polega na tym, że funkcja sinus nie ma granicy dla $n\to+\infty$ , dlatego będziemy się posiłkować twierdzeniem o dwóch ciągach.
Mamy $\sin{n}\leq 1$ dla wszystkich $n$ naturalnych. Zatem $(3\sin{n}-5)\cdot n^3\leq (3\cdot 1-5)\cdot n^3$ $=-2n^3\leq -n\stackrel{n\to \infty}{\longrightarrow}-\infty$ .
Ponieważ ciąg o wyrazach większych jest rozbieżny do $-\infty$ , zatem $\lim_{n\to \infty}{(3\sin{n}-5)\cdot n^3}$ $=-\infty$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\left(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\dots +\frac{1}{\sqrt{n}}\right)}$ .
Rozwiązanie: Zauważmy, że każdy wyraz ciągu jest sumą ułamków postaci $\frac{1}{\sqrt{k}}$ oraz, że składników sumy w $n$ -tym wyrazie ciągu jest dokładnie $n$ . Oszacujmy $\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\dots +\frac{1}{\sqrt{n}}$ $\geq \frac{1}{\sqrt{n}}\cdot n$ $= \sqrt{n} \stackrel{n\to \infty}{\longrightarrow}+\infty$ , zatem $\lim_{n\to \infty}{\left(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\dots +\frac{1}{\sqrt{n}}\right)}$ $=+\infty$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\frac{\left((-1)^n-2\right)n^2}{n+1}}$ .
Rozwiązanie: Zauważmy, że zawsze jest $(-1)^n\leq 1$ . Mamy $\frac{\left((-1)^n-2\right)n^2}{n+1}$ $\leq \frac{\left(1-2\right)n^2}{n+1}$ $=\frac{-n^2}{n+1}$ $=\stackrel{n\to \infty}{\longrightarrow}-\infty$ . Zatem $\lim_{n\to \infty}{\frac{\left((-1)^n-2\right)n^2}{n+1}}$ $=-\infty$ .

Twierdzenie o trzech ciągach

Twierdzenie (O trzech ciągach)
Jeżeli $\lim_{n\to \infty}{a_n}=g=\lim_{n\to \infty}{c_n}$ oraz od pewnego miejsca zachodzi nierównośc pomiędzy wyrazami trzech ciągów $a_n\leq b_n\leq c_n$ , to ciąg $(b_n)$ jest zbieżny i $\lim_{n\to \infty}{b_n}=g$ .

Komentarz
Żartobliwie nazywa się twierdzenie o trzech ciągach "twierdzeniem o mnie i dwóch policjantach": jeśli dwóch policjantów idzie na komisariat i ja idę między nimi, to ja też idę na komisariat.

Rysunek przedstawia trzy ciągi. Zielony i niebieski mają granicę 0.5, zatem ciąg czerwony, ograniczony przez dwa pozostałe, również ma granicę 0.5.

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\frac{n^2+n-\cos{n^2}}{2+n\sin{\sqrt{n}}+3n^2}}$ .
Rozwiązanie: Kłopot polega na tym, że wyrazy ciągu zawierają sinus i cosinus, które to funkcje nie mają granicy w nieskończoności, dlatego pozbędziemy sie ich poprzez oszacowania $-1\leq \sin{\sqrt{n}}\leq 1$ oraz $-1\leq \cos{n^2}\leq 1$ , prawdziwe dla każdego $n$ naturalnego. Mamy
$\frac{1}{3}\stackrel{n\to \infty}{\longleftarrow}\frac{n^2\left(1+\frac{1}{n}-\frac{1}{n^2}\right)}{n^2\left(\frac{2}{n^2}+\frac{1}{n}+3\right)}$ $=\frac{n^2+n-1}{2+n+3n^2}$ $\leq \frac{n^2+n-\cos{n^2}}{2+n\sin{\sqrt{n}}+3n^2}$ $\leq \frac{n^2+n+1}{2-n+3n^2}$ $=\frac{n^2\left(1+\frac{1}{n}+\frac{1}{n^2}\right)}{n^2\left(\frac{2}{n^2}-\frac{1}{n}+3\right)}\stackrel{n\to \infty}{\longrightarrow}\frac{1}{3}$ . Zatem $\lim_{n\to \infty}{\frac{n^2+n-\cos{n^2}}{2+n\sin{\sqrt{n}}+3n^2}}$ $=\frac{1}{3}$ .

Granice niektórych ciągów i granice specjalne

Twierdzenie (O granicy ciągu stałego)
Zachodzi $\lim_{n\to \infty}{a}=a$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\frac{(3n-9)(n+1)}{n^2-2n-3}}$ .
Rozwiązanie: Mamy $\lim_{n\to \infty}{\frac{(3n-9)(n+1)}{n^2-2n-3}}$ $=\lim_{n\to \infty}{\frac{3(n-3)(n+1)}{(n-3)(n+1)}}$ $=\lim_{n\to \infty}{3}$ $=3$ .

Twierdzenie (O granicy ciągu geometrycznego)
$\lim_{n\to \infty}{q^n}=\begin{cases}0\text{, dla }|q|<1\\ 1\text{, dla }q=1\\+\infty\text{, dla }q>1\\ \textrm{nie istnieje, dla }q\leq -1\end{cases}$ .

Uwaga
Ciąg geometryczny $q^n$ jest zbieżny jedynie dla $q \in (-1,1]$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\frac{2\cdot 3^{n+1}+4^{1-n}+2^{3n+2}}{5^{n-1}+4^{n+2}+3\cdot 8^{n-1}}}$ .
Rozwiązanie: Mamy $\lim_{n\to \infty}{\frac{2\cdot 3^{n+1}+4^{1-n}+2^{3n+2}}{5^{n-1}+4^{n+2}+3\cdot 8^{n-1}}}=$ {"odszyfrowujemy" wykładniki} $=\lim_{n\to \infty}{\frac{6\cdot 3^n+4\cdot \left(\frac{1}{4}\right)^n+4\cdot 8^n}{\frac{1}{5}\cdot 5^n+16\cdot 4^n+\frac{3}{8}\cdot 8^n}}=$ {wyłączamy z licznika i mianownika dominantę mianownika} $=\lim_{n\to \infty}{\frac{8^n\left(6\cdot \left(\frac{3}{8}\right)^n+4\cdot \left(\frac{1}{32}\right)^n+4\right)}{8^n\left(\frac{1}{5}\cdot \left(\frac{5}{8}\right)^n+16\cdot \left(\frac{1}{2}\right)^n+\frac{3}{8}\right)}}$ $=\left[\frac{6\cdot 0+4\cdot 0+4}{\frac{1}{5}\cdot 0+16\cdot 0+\frac{3}{8}}\right]$ $=\frac{32}{3}$ .

Twierdzenie (O granicy pierwiastka stopnia n-tego ze stałej)
$\lim_{n\to \infty}{\sqrt[n]{q}}=1$ , dla $q>0$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\sqrt[n]{2+3^{n+1}+4^{n-1}+2\cdot 5^{1-n}}}$ .
Rozwiązanie: Mamy $\sqrt[n]{2+3^{n+1}+4^{n-1}+2\cdot 5^{1-n}}=$ {"odszyfrujmy" wykładniki} $=\sqrt[n]{2+3^{n}\cdot 3+4^{n}\cdot \frac{1}{4}+10\cdot \left(\frac{1}{5}\right)^n}$ . Aby skorzystać z twierdzenia o trzech ciągach wykonajmy szacowanie
$\sqrt[n]{\frac{1}{4}\cdot 4^n}$ $\leq \sqrt[n]{2+3^{n}\cdot 3+4^{n}\cdot \frac{1}{4}+10\cdot \left(\frac{1}{5}\right)^n}$ $\leq \sqrt[n]{2\cdot 4^n+4^n\cdot 3+4^n\cdot \frac{1}{4}+10\cdot 4^n}$ .
Granica lewej strony: $\lim_{n \to \infty}{\sqrt[n]{\frac{1}{4}\cdot 4^n}}$ $=\lim_{n \to \infty}{4 \cdot \sqrt[n]{\frac{1}{4}}}$ $=[4 \cdot 1]$ $=4$ .
Granica prawej strony: $\lim_{n\to \infty}{\sqrt[n]{2\cdot 4^n+4^n\cdot 3+4^n\cdot \frac{1}{4}+10\cdot 4^n}}$ $=\lim_{n\to \infty}{\sqrt[n]{15\frac{1}{4}\cdot 4^n}}$ $=\lim_{n\to \infty}{4\cdot \sqrt[n]{15\frac{1}{4}}}$ $=[4\cdot 1]$ $=4$ .
Zatem musi być: $\lim_{n\to \infty}{\sqrt[n]{2+3^{n+1}+4^{n-1}+2\cdot 5^{1-n}}}$ $=4$ .

Twierdzenie (O granicy pierwiastka stopnia $n$ -tego z liczby $n$ )
$\lim_{n\to \infty}{\sqrt[n]{n}}=1$ .

Przykład
Obliczmy granicę $\lim_{n\to \infty}{\frac{1}{\sqrt[n]{n}-1}}$ .
Rozwiązanie: Ponieważ $\sqrt[n]{n}-1>0$ mamy $\lim_{n\to \infty}{\frac{1}{\sqrt[n]{n}-1}}$ $=\left[\frac{1}{1^+-1}\right]$ $=\left[\frac{1}{0^+}\right]$ $=+\infty$ .

Twierdzenie (O własnościach ciągu $\left(1+\frac{1}{n}\right)^n$ )
Ciąg $\left(1+\frac{1}{n}\right)^n$ jest rosnący, ograniczony i zbieżny do granicy $e$ .

Uwaga
Liczbę $e\approx 2,718281828459...$ nazywamy liczbą Eulera lub Nepera.

Rysunek przedstawia kolejne wyrazy ciągu $\left(1+\frac{1}{n}\right)^n$ .

Przykład
Obliczmy granicę ciągu $\left(\frac{n}{n+1}\right)^n$ .
Rozwiązanie: Mamy $\lim_{n\to \infty}\left(\frac{n}{n+1}\right)^n$ $=\left[1^{\infty}\right]$ $=\lim_{n\to \infty}\left(\frac{n+1}{n}\right)^{-n}$ $=\lim_{n\to \infty}\left[\left(1+\frac{1}{n}\right)^n\right]^{-1}$ $=e^{-1}$ .

dostęp do własnych plusów, ocen, obecności i materiałów dydaktycznych po zalogowaniu

3 ms - 22915 wyświetleń